ELEARNING - FREIBURG

HOME   Mathematik   Prüfungsaufgaben

♦ Abikurs Mathe - Analysis ♦

<< 20 - Integrale - Rotationskörper >>


Lässt man den Graphen einer Funktion f(x) um die x-Achse rotieren, so entsteht ein Rotationskörper, dessen Volumen man in einem vorgegeben Intervall [a;b] bestimmen kann.

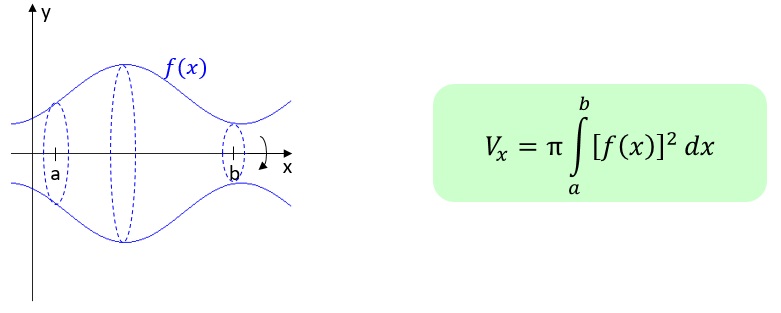
Häufig entstehen unter dem Integralzeichen Ausdrücke, die Sie nicht "von Hand" berechnen können, da in der Schule die entsprechenden Techniken schon seit Jahren nicht mehr vermittelt werden. Hier hilft Ihnen nur noch der Taschenrechner (GTR oder Casio ClassPad).

Hinweis:
Die Berechnung von Rotationskörpern, die durch Rotation eines Graphen um die y-Achse entstehen, kommen so selten vor, dass wir diese hier NICHT behandeln!

Rechenbeispiel 1

Berechne Vx im Intervall [0;2] für f(x)=x2.

Lösung

Rechenbeispiel 2

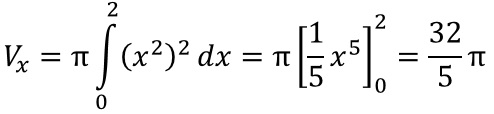
Berechne Vx im Intervall [0;2] für .

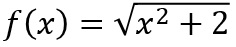Lösung


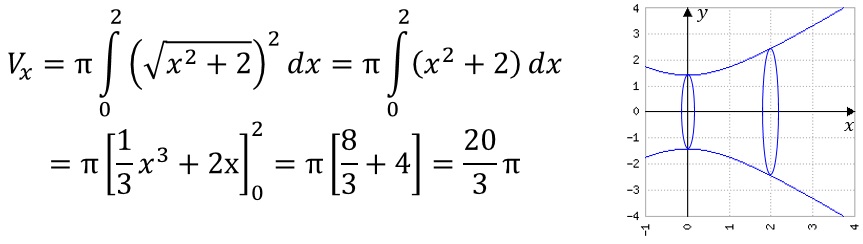
Rotationskörper: ft(x)=t·cos(x); -π/2≤x≤π/2.
Das Schaubild von ft schließt mit der x-Achse eine Fläche ein.
Bei Rotation dieser Fläche um die x-Achse entsteht ein Dreh-körper.
Berechnen Sie dessen Volumen in Abhängigkeit von t.

Lösung


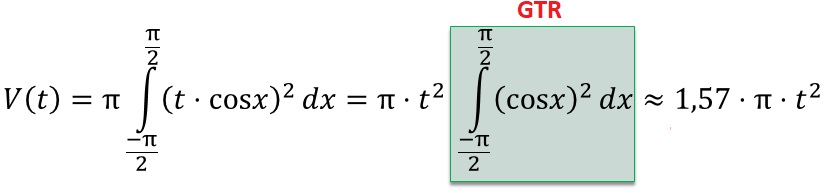
Rotation um parallele Achsen

Wie berechnet man das Volumen eines Rotationskörpers, der um eine Parallele zur x-Achse rotiert?

Lösung:
  • Verschiebe f(x) so, dass die neue Funktion g(x) um die x-Achse rotiert.
  • Berechne Vx mit der bekannten Formel.
Die Berechnungen sind meist sehr aufwändig. Entsprechend selten kommt diese Aufgabenstellung im Abitur vor.

Downloads

PowerPoint
PDF